Let 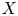X$X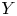$, Y$Y$ be nonsingular real algebraic sets. A map 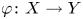\varphi \colon X \to Y$\varphi \colon X \to Y$ is said to be 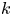k$k$-regulous, where 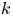k$k$ is a nonnegative integer, if it is of class 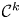\mathcal {C}^k$\mathcal {C}^k$ and the restriction of 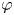\varphi$\varphi$ to some Zariski open dense subset of 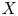X$X$ is a regular map. Assuming that 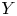Y$Y$ is uniformly rational, and 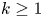k \geq 1$k \geq 1$, we prove that a \mathcal {C}^{\infty }$\mathcal {C}^{\infty }$ map 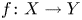f \colon X \to Y$f \colon X \to Y$ can be approximated by 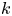k$k$-regulous maps in the 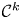\mathcal {C}^k$\mathcal {C}^k$ topology if and only if 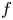f$f$ is homotopic to a 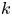k$k$-regulous map. The class of uniformly rational real algebraic varieties includes spheres, Grassmannians and rational nonsingular surfaces, and is stable under blowing up nonsingular centers. Furthermore, taking Y=\mathbb {S}^p$Y=\mathbb {S}^p$ (the unit 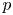p$p$-dimensional sphere), we obtain several new results on approximation of 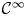\mathcal {C}^{\infty }$\mathcal {C}^{\infty }$ maps from 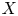X$X$ into 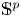\mathbb {S}^p$\mathbb {S}^p$ by 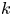k$k$-regulous maps in the 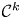\mathcal {C}^k$\mathcal {C}^k$ topology, for 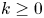k \geq 0$k \geq 0$.

We prove a large finite field version of the Boston–Markin conjecture on counting Galois extensions of the rational function field with a given Galois group and the smallest possible number of ramified primes. Our proof involves a study of structure groups of (direct products of) racks.

We generalize bounds of Liu–Wan–Xiao for slopes in eigencurves for definite unitary groups of rank 2$2$ to slopes in eigenvarieties for definite unitary groups of any rank. We show that for a definite unitary group of rank n$n$, the Newton polygon of the characteristic power series of the U_p$U_p$ Hecke operator has exact growth rate x^{1+2/{n(n-1)}}$x^{1+2/{n(n-1)}}$, times a constant proportional to the distance of the weight from the boundary of weight space. The proof goes through the classification of forms associated to principal series representations. We also give a consequence for the geometry of these eigenvarieties over the boundary of weight space.

We prove a Tannakian form of Drinfeld's lemma for isocrystals on a variety over a finite field, equipped with actions of partial Frobenius operators. This provides an intermediate step towards transferring V. Lafforgue's work on the Langlands correspondence over function fields from \ell$\ell$-adic to p$p$-adic coefficients. We also discuss a motivic variant and a local variant of Drinfeld's lemma.

We study finite orbits of non-elementary groups of automorphisms of compact projective surfaces. We prove that if the surface and the group are defined over a number field \mathbf {k}$\mathbf {k}$ and the group contains parabolic elements, then the set of finite orbits is not Zariski dense, except in certain very rigid situations, known as Kummer examples. Related results are also established when \mathbf {k} = \mathbf {C}$\mathbf {k} = \mathbf {C}$. An application is given to the description of ‘canonical vector heights’ associated to such automorphism groups.

Fix a prime p\geq 11$p\geq 11$. We show that there exists a positive integer m$m$ such that any subset of \mathbb {F}_p^n\times \mathbb {F}_p^n$\mathbb {F}_p^n\times \mathbb {F}_p^n$ containing no nontrivial configurations of the form (x,y)$(x,y)$, (x,y+z)$(x,y+z)$, (x,y+2z)$(x,y+2z)$, (x+z,y)$(x+z,y)$ must have density \ll 1/\log _{m}{n}$\ll 1/\log _{m}{n}$, where \log _{m}$\log _{m}$ denotes the m$m$-fold iterated logarithm. This gives the first reasonable bound in the multidimensional Szemerédi theorem for a two-dimensional four-point configuration in any setting.